時間に伴う故障率の変化
起きる故障の種類は設備を使用している経過時間によって性質が異なる。この故障の発生確率を縦軸に、経過時間を横軸にとると以下のようなグラフになる。
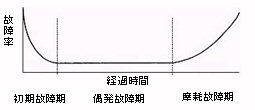
バスタブカーブ
その形から「バスタブカーブ」と呼ばれるこの曲線は、期間を3つに分けて時間の早い順に以下のように呼ばれる。
①初期故障期
②偶発故障期
③摩耗故障期
確率分布の中の、ワイブル分布
ワイブル分布は、スウェーデンのワイブルが鋼の破壊強度の分布を表すために使用し始めたもの。
この分布は形状パラメータmの値によって、初期故障期、偶発故障期、摩耗故障期の故障分布にあてはめることができる。
機械の寿命、材料の破壊強度、システムの寿命等を測るとき用いられる。
m:形状パラメータ、η:尺度パラメータ、γ:位置パラメータ
・・・3パラメータワイブル分布と言ったりする
信頼度 R(t)=exp(-((t-γ)/η)^m)) (t>=γ,m>0,η>0)
・・・γはその時間まで故障が起きないとされる時間、(γ=0なら最初から故障が起こり始める)
不信頼度 F(t)=1-R(t)=1-exp(-((t-γ)/η)^m))
故障密度関数 f(t)=F'(t)=(m/η)((t-γ)/η)^(m-1)) * exp(-((t-γ)/η)^m))
(t(時間)>=0,m>0)
故障率 λ(t)=f(t)/R(t)=(m/η)((t-γ)/η)^(m-1))
上記の式表わされる故障率は、mの値によって分布形状が変わる。
m=1の時、λ(t)=1/ηとなり、一定になります。これは、偶発故障を表す。
m>1の時、λ(t)は時間とともに増加します。これは、摩耗故障を表す。
m<1の時、λ(t)は時間とともに減少します。これは、初期故障を表す。
ワイブル解析
ワイブル解析は、故障データの解析によって、初期故障期なのか、偶発故障期なのか、または、摩耗故障期なのかが判定できる。
設備修理の程度や更新の要・不要の判断に有効であるほか、設備を稼働させるときになるべく初期故障期間ではなく、偶発故障期間で稼働させたいとき等にも使う。
得られた故障データから解析を行う。
γ=0とすると、信頼度R(t)は
1-F(t)=exp(-(t/η)^m))
両側の対数を取る。
ln(1-F(t))=ln(exp(-(t/η)^m)))=-(t/η)^m
-ln(1-F(t))=(t/η)^m
もう一度両側の対数を取る。
ln(-ln(1-F(t)))=ln((t/η)^m)=mln(t/η)=mlnt-mlnη
なぜこんな計算をするのかというと、直線であらわせるグラフを作るため。
「ワイブル確率紙」は両対数でX軸がlnt、Y軸がln(-ln(1-F(t)))になっている。
つまり、上記の式は
Y=mX-Bのような直線になる。(B=mlnη)
γ=0にならないと直線にならない。ワイブル確率紙にプロットするときはγ=0になるようにtを補正しておく。

ワイブル確率へのプロット